Elementare Wahrscheinlichkeit [1]

Axiome von Kolgorow

Für jedes Ereignis \(A \in \Sigma\) und \(B \in \Sigma\) gilt:

  1. \(P(A) \geq 0\)
  2. \(P(\Omega) = 1\)
  3. \(A \cap B = \emptyset \to P(A \cup B) = P(A) + P(B)\)

Definitionen

  • Potenzmenge \(\Sigma\) (lies Sigma) ist die Grundmenge bzw. Ergebnisraum
  • Ergebnismenge \(\Omega\) (lies Omega) ist die Menge aller Ergebnisse eines Zufallsexperiments
  • \(\Sigma = \{\emptyset, \Omega\} + \Omega\)

Folgerungen aus Kolgorow’s Axiomen

Für jedes Ereignis \(A \in \Sigma\) und \(B \in \Sigma\) gilt:

  1. \(P(\Omega \setminus A) = 1 - P(A)\)
  2. \(P(\emptyset) = 0\)
  3. \(P(A \cup B) = P(A) + P(B) + P(A \cap B)\)
  4. \(P(A \cup B) = P(A \setminus B) + P(A \cap B) + P(B \setminus B)\)
  5. \(P(A) = P(A \setminus B) + P(A \cap B)\)
  6. \(P(B) = P(B \cap A) + P(B \setminus A)\)
  7. \(P(A) + P(B) = P(A \cup B) + P(A \cap B)\)

Laplace-Experiment

Ein Zufallsexperiment heisst Laplace-Experiment, wenn alle Elementarereignisse die gleiche Wahrscheinlichkeit besitzen.

\(\displaystyle \omega \in \Omega: P(\{\omega\}) = \frac{1}{|\Omega|}\)

\(|\Omega|\) ist die Mächtigkeit von \(\Omega\), also die Anzahl Elemente

Beispiele

Würfelwurf: \(P(\{2\}) = \frac{1}{6}\)

Münzwurf: \(P(\{Kopf\}) = \frac{1}{2}\)

Roulette: \(P(\{17\}) = \frac{1}{37}\)

Mehrstufiges Zufallsexperiment

Wird ein Zufallsexperiment mehrmals durchgeführt oder werden verschiedene Zufallsexperimente nacheinander ausgeführt, so kann man dies als einmalige Ausführung eines mehrstufigen Zufallsexperiments auffassen. Wir stellen ein mehrstufiges Zufallsexperiment mithilfe eines Baumdiagramms dar.

Beispiel: In einer Urne liegen 7 blaue und 3 rote Kugeln. Es werden nacheinander 2 Kugeln mit Zurücklegen gezogen.

1. Experiment: Ziehung der 1. Kugel mit \(\Omega_1 = \{r, b\}\)

2. Experiment: Ziehung der 2. Kugel mit \(\Omega_2 = \{r, b\}\)

2-stufiges Experiment: \(\Omega = \{rr, rb, br, bb\}\)

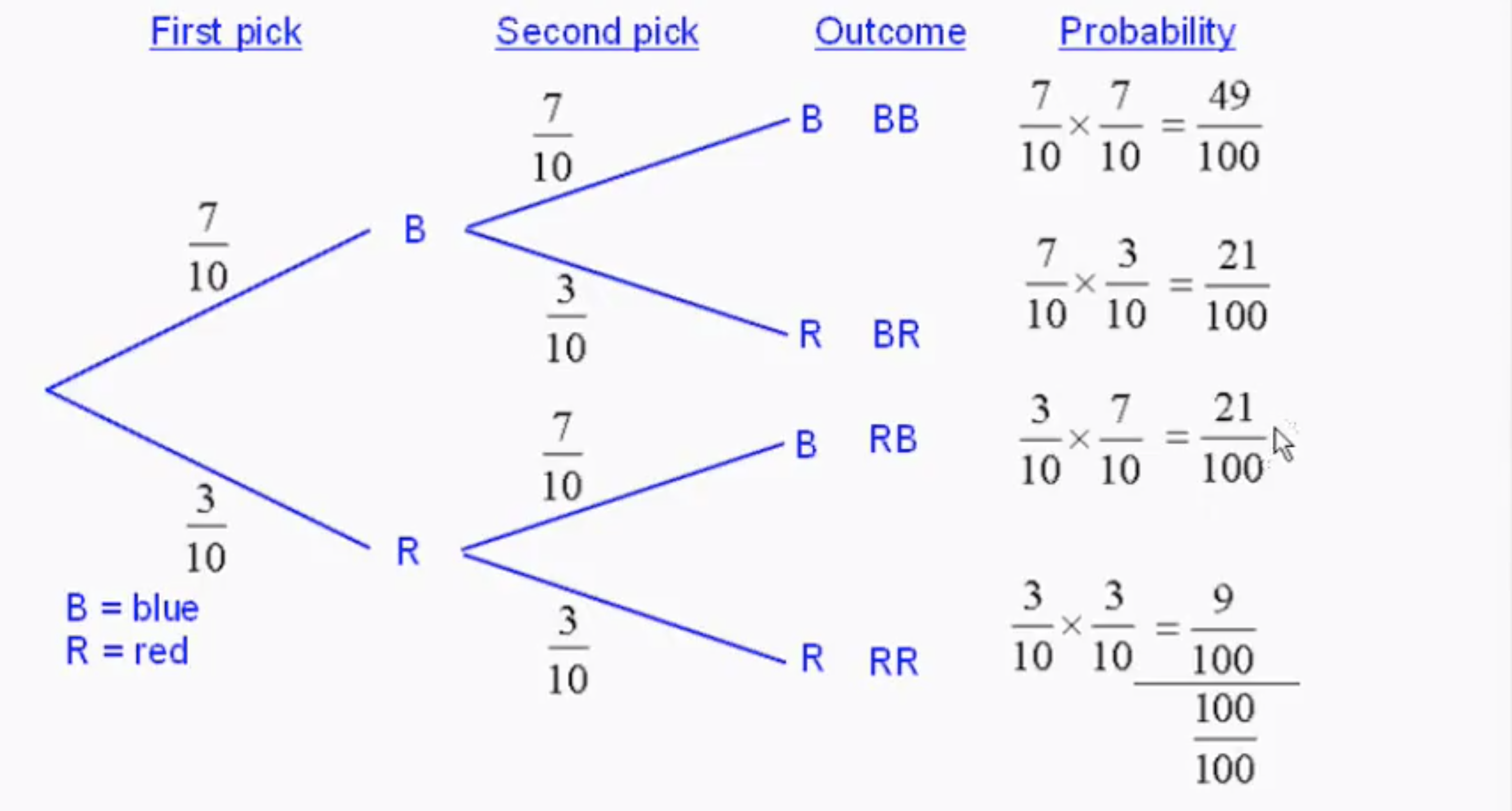
../_images/tree.png

[2]

Ein Pfad im Baumdiagramm ist ein Weg ausgehend vom Anfangspunkt entlang von Ästen zu einem Endpunkt.

1. Pfadregel: Wahrscheinlichkeiten entlang eines Pfades werden multipliziert.

2. Pfadregel: Wahrscheinlichkeiten verschiedener Pfade werden addiert.

1. Baumregel: Die Summe der Wahrscheinlichkeiten auf den Ästen, die von einem gemeinsamen Anfangspunkt ausgehen, ist stets 1.

2. Baumregel Die Summe der Wahrscheinlichkeiten aller Pfade ist 1.

Bedingte Wahrscheinlichkeit

Definition Kolgorow’s

\(\displaystyle P(A|B) = \frac{P(A \cap B)}{P(B)}\)

| bedeutet ‘unter der Bedingung von’.
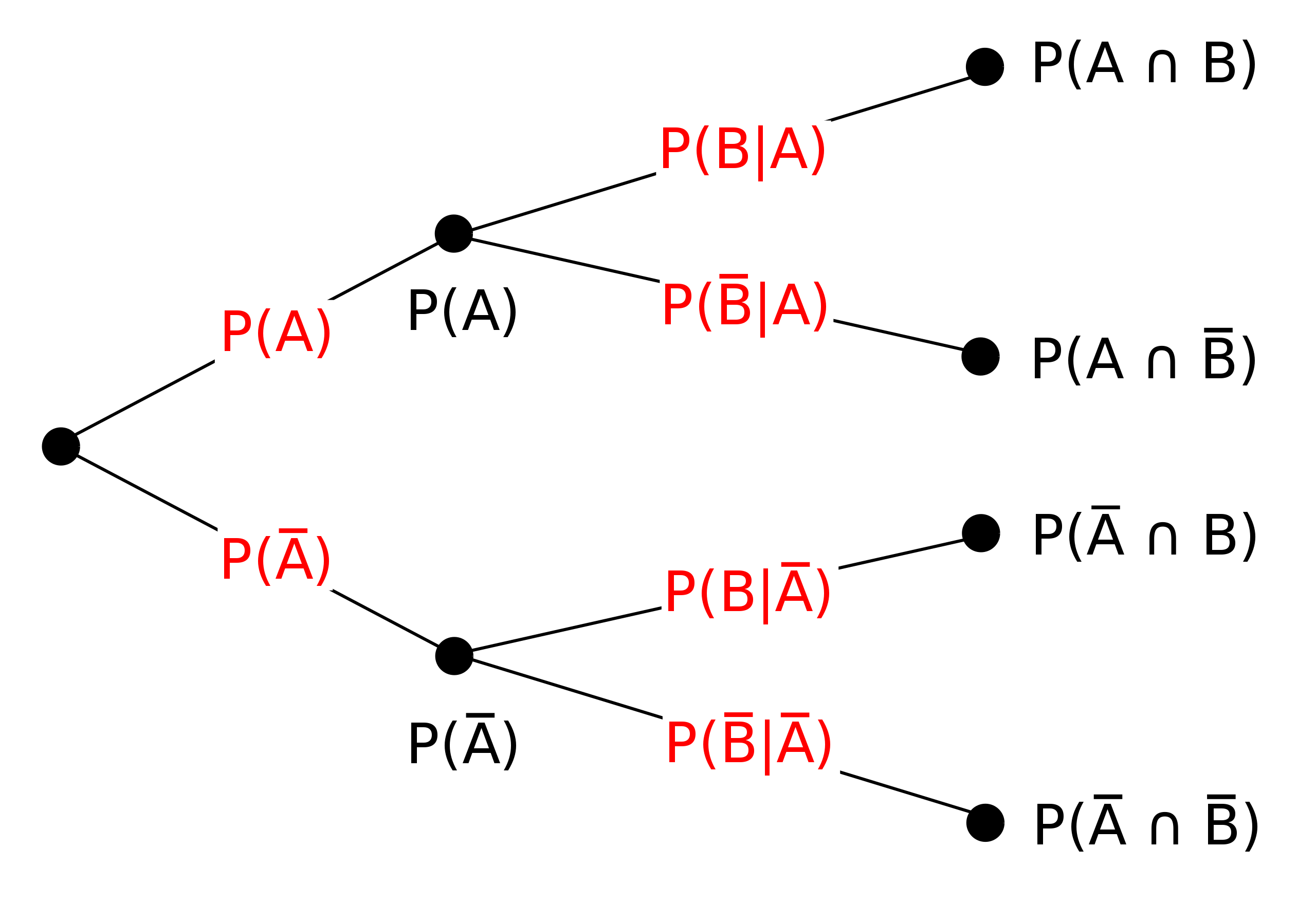
../_images/cond_prob.png

Beispiel: Die Wahrscheinlichkeit, dass eine Rose-Zahlenkarte aus einem Jasskartenset gezogen wurde, wenn schon bekannt ist, dass eine Rose-Karte gezogen wurde, ist:

\[P(Zahl|Rose) = \frac{P(Zahl \cap Rose)}{P(Rose)} = \frac{\frac{4}{36}}{\frac{9}{36}} = \frac{4}{9}\]

Folgerungen

  1. \(P(A \cap B) = P(A|B) \cdot P(B) = P(B|A) \cdot P(A)\)
  2. Satz von Bayes: \(\displaystyle P(A|B)= \frac{P(B|A) \cdot P(A)}{P(B)}\)

Unabhängigkeit von Ereignissen

\(A\) und \(B\) sind unabhängig, wenn \(P(A\cap B)=P(A)\cdot P(B)\)

Zufallsgrösse

Gegeben ist ein Zufallsexperiment mit dem Ergebnisraum \(\Omega\). Eine Zufallsgrösse \(X\) ist eine Funktion, die jedem Ergebnis \(\omega \in \Omega\) eine reelle Zahl \(X(\omega)\) zuordnet.

Bernoulliketten

Bernoulliexperiment

Ein Zufallsexperiment mit nur zwei möglichen Ergebnissen: Treffer \(T\) und Niete \(N\)

Erfolgswahrscheinlichkeit \(p = P(T)\)

Misserfolgswahrscheinlichkeit \(P(N) = (1-p)\)

Jedes Zufallsexperiment kann zu einem Bernoulliexperiment umgeformt werden. Ist \(\Omega\) die Ergebnismenge, so zeichnen wir ein spezielles Ereignis \(T \subset \Omega\) aus und betrachten nur noch die Versuchsausgänge \(T\) und \(\overline{T}=N\).

Bernoullikette der Länge \(n \in \mathbb{N}\)

Ein Bernoulliexperiment wir \(n\)-mal wiederholt. Die Ergebnismenge \(\Omega\) besteht aus allen Sequenzen der Länge \(n\) aus den Buchstaben \(T\) und \(N\). Die Mächtigkeit von \(\Omega\) ist \(|\Omega| = 2^n\).

\(A =\) Kein Treffer: \(P(A) = (1-p)^n\)

\(B =\) Mindestens ein Treffer: \(P(B) = 1-(1-p)^n\)

\(C =\) genau \(k\) Treffer: \(P(C)=\binom{n}{k}\cdot p^k\cdot (1-p)^{n-k}\)

Wartezeit-Aufgaben

Erster Treffer:

Die Zufallsgrösse \(X\) beschreibt, im wievielten Versuch erstmals ein Treffer eintritt.

  • Wahrscheinlichkeit für den ersten Treffer im \(n\)-ten Versuch. Bzw. Wahrscheinlichkeit, dass die ersten \(n-1\) Versuche Nieten und der \(n\)-ten Versuch ein Treffer ergeben:

    \[P(X=n) = (1-p)^{n-1} \cdot p\]

  • Wahrscheinlichkeit für den ersten Treffer frühestens im \(n\)-ten Versuch. Bzw. Wahrscheinlichkeit für keinen Treffer in den ersten \(n-1\) Versuchen:

    \[P(X=n) = (1-p)^{n-1}\]

  • Wahrscheinlichkeit für den ersten Treffer spätestens im \(n\)-ten Versuch. Bzw. Wahrscheinlichkeit, dass nicht alle \(n\) Versuche Nieten sind.

    \[P(X=n) = 1 - (1-p)^n\]

Beispiel: Würfelwurf, Treffer ist Ereignis \(T = {1, 2}\). Die Zufallsgrösse \(X\) beschreibt, im wievielten Versuch \(T\) erstmals eintritt. \(P(T) = p = \frac{1}{3}.\)

  • \(P(X=5) = (1-\frac{1}{3})^{4} \cdot \frac{1}{3} = \frac{16}{243}\)
  • \(P(X\geq 5) = (1-\frac{1}{3})^{4} = \frac{16}{81}\)
  • \(P(X\leq 5) = 1 - (1-\frac{1}{3})^{5} = 1 - \frac{32}{243} = \frac{211}{243}\)
Suche nach Länge \(n\) der Bernoullikette:

Die Zufallsgrösse \(Y\) beschreibt die Anzahl Treffer mit Erfolgswahrscheinlichkeit \(p\) bei einer Bernoullikette der Länge \(n\).

  • Was ist die kleinste Anzahl Versuche (kleinstes \(n\)), dass zu einer Wahrscheinlichkeit von mindestens \(A\) mindestens ein Treffer eintritt? Bzw. dass zu einer Wahrscheinlichkeit von höchstens \(1-A\) kein Treffer eintritt?

    \[\begin{split}\begin{align} P(Y\geq 1)& \geq A\\ \Leftrightarrow 1 - P(Y=0)& \geq A\\ \Leftrightarrow 1-A& \geq P(Y=0)\\ \Leftrightarrow 1-A& \geq (1-p)^n\\ \Leftrightarrow \log(1-A)& \geq n \cdot \log(1-p)\\ \Leftrightarrow \displaystyle \frac{\log(1-A)}{\log(1-p)}& \leq n\\ \end{align}\end{split}\]

    Warning

    Siehe Logarithms 4 für die Logarithmusgesetze.

    Im letzten Schritt wird durch \(\log(1-p)\) geteilt, beachte, dass der Logarithmus einer Zahl zwischen 0 und 1 negativ ist und deshalb Ungleichheitszeichen gekehrt werden muss.

Beispiel: Würfelwurf, Treffer ist Ereignis \(T = {1, 2}\). \(expression\): Anzahl Treffer. Wie oft muss gewürfelt werden, dass zu einer Wahrscheinlichkeit von \(97%\) mindestens eine 1 oder eine 2 gewürfelt wird?

  • \(P(Y\geq 1) \geq 0.97 \Leftrightarrow \displaystyle n \geq \frac{\log(0.03)}{\log(\frac{2}{3})} \approx 8.65\)

    Es muss mindestens 9 mal gewürfelt werden, damit zu einer \(97%\)-iger Wahrscheinlichkeit mindestens eine 1 oder eine 2 gewürfelt wird.

[1]Sources: https://de.wikipedia.org/wiki/Wahrscheinlichkeitstheorie, Dr. Robert Aehle
[2]https://www.youtube.com/watch?v=mkDzmI7YOx0